Research nuggets#
Below we provide brief descriptions of some of the current projects. The list is incomplete and updates appear regularly.
For more, please take a look at the list of publications, software and other sections from the menu on the left.
|
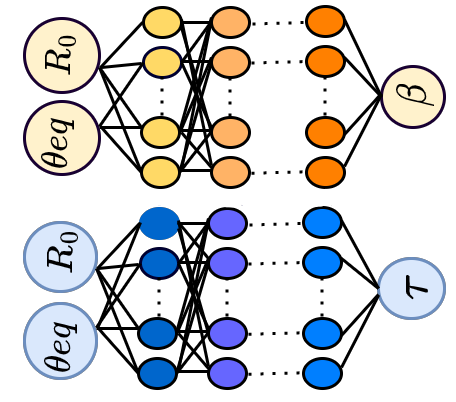
Machine learning based data-driven discovery of non-linear phase-field dynamics Project descriptionOne of the primary questions regarding complex systems at a large scales is how the detailed microscopic properties give rise to effective interactions and driving forces. Coarse-grained models are designed to describe complex systems using simplified equations with fewer degrees of freedom. Traditionally, equations of motion or dynamic equations have been constructed based on knowledge of basic properties such as symmetries, dimensionality and conservation laws. Machine learning (ML) offers a new alternative as it can be used to identify the governing equations directly from data. This is a new and rapidly developing field, and despite many advances, it remains challenging to discover partial differential equations (PDEs) that involve high-order derivatives directly from data. In our work, we have introduced novel data-driven architectures that employ multi-layer perceptron (MLP), convolutional neural networks (CNN), and a combination of CNN and long short-term memory (CNN-LSTM) structures to uncover the non-linear equations of motion for phase-field models with both conserved and non-conserved order parameters. We consider two distinct scenarios: (i) There is an unknown relation between field evolution and its spatial derivatives. For the first scenario, a flexible framework that can deal with large data sets and extract the unknown PDE(s) is developed. Two different approaches are presented for learning coarse-scale PDEs: 1) an MLP architecture and 2) a CNN-LSTM. For the second scenario, a convolutional neural network (CNN) is used to implicitly learn the dependence of the time derivative of the field on the spatial derivative(s) of unknown orders. The well-known Allen-Cahn, Cahn-Hilliard, and the phase-field crystal (PFC) models were used as the test cases. We show that not only can we effectively learn the time derivatives of the field in both scenarios, but we can also use the data-driven PDEs to propagate the field in time and achieve results in good agreement with the original PDEs. We have also developed a general purpose code SymPhas for phase-field simulations (open source). References:
|
|
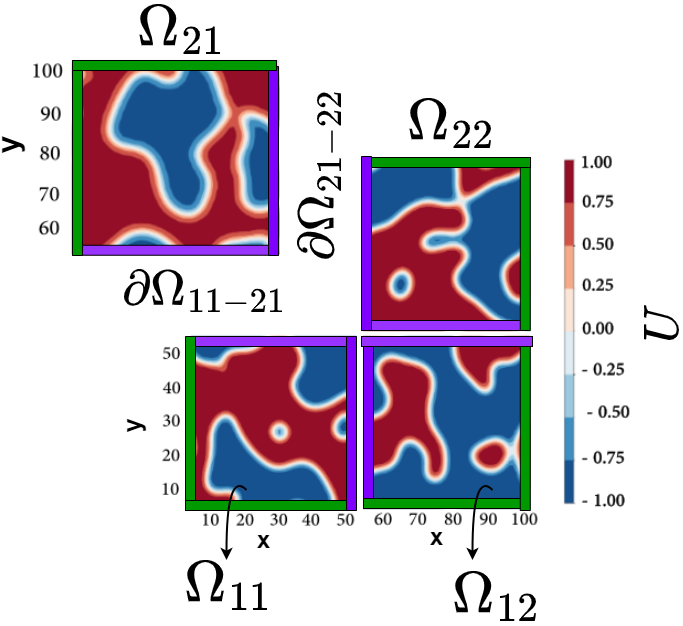
A Framework Based on Symbolic Regression Coupled with eXtended Physics-Informed Neural Networks (X-PINNs) for Gray-Box Learning of Equations of Motion from Data Project descriptionPartial differential equations (PDEs) are commonly used for modeling the evolution of dynamical systems in, e.g., fluid dynamics, heat transfer, financial derivatives, chemical reactions and phase transformations. From the physical perspective, one of the main problems is constructing models that contain all the relevant information about the system at hand. This involves, for example, identifying the order parameters, relevant symmetries and possible couplings, and their nature, between the order parameters. Machine learning (ML) offers a method for automated construction of models directly from experimental or other data: it can be used to identify PDEs from data without prior/or only with partial knowledge about the underlying physics. Physics-Informed Neural Networks (PINNs) [1] is a class of ML algorithms that integrates the governing dynamic equations of a system into a neural network architecture. One of the significant advantages of PINNs is that they are capable of discovering unknown equations that govern a system from data. This is achieved by incorporating physics-based regularization terms in the loss function used to train the neural network, which enables the network to learn both from observed data and the underlying physics principles. Our framework [2] for discovering the unknown components of nonlinear equations directly from data employs eXtended Physics-Informed Neural Networks (X-PINNs) [3], and involves generalized space-time domain decomposition in order to provide computationally efficient solutions to PDEs across large spatial and temporal domains. The overall domain is partitioned into smaller subdomains, and PINNs are used to solve the PDEs in each subdomain. Continuity conditions at the interfaces between the subdomains are enforced as soft constraints in the loss function. This approach allows us to efficiently handle large-scale PDE problems with high accuracy and computational efficiency. After discovering the unknown term and collecting data from phase-field simulations, we utilize a symbolic regression model to predict the explicit mathematical formula of the unknown term. Symbolic regression [4] is a machine learning technique that is specifically designed to uncover mathematical equations or expressions that fit a given dataset. By applying symbolic regression to the data obtained from phase-field simulations and the discovered term, we can accurately identify the mathematical formula that best describes the unknown term. This approach enables us to gain deeper insights into the underlying physics of the system and can aid in the development of more accurate predictive models. References:
|
|
Computational and theoretical modeling of cancer growth and tumour response on radiation therapy Project descriptionRadiation therapy is one of the most common cancer treatments and, historically, it emerged from interdisciplinary research combining oncology, molecular biology, physics, mathematics, chemistry and imaging. Radiation therapy is a very common treatment. It is estimated that about 70% of cancer patients receive it. Radiation therapy functions by damaging and killing cancer cells via ionizing radiation which causes molecular level damage manifested in the mechanobiological properties of (cancer) cells.
Radiation is not selective: It damages both cancerous and healthy cells. This makes dose optimization and targeting of radiation crucial. The aim of this research is to understand the fundamental nature of mechanobiology and its relation to cancer growth and metastasis using quantitative and predictive computational modeling, machine learning and data from radiation therapy experiments. References:
|
|
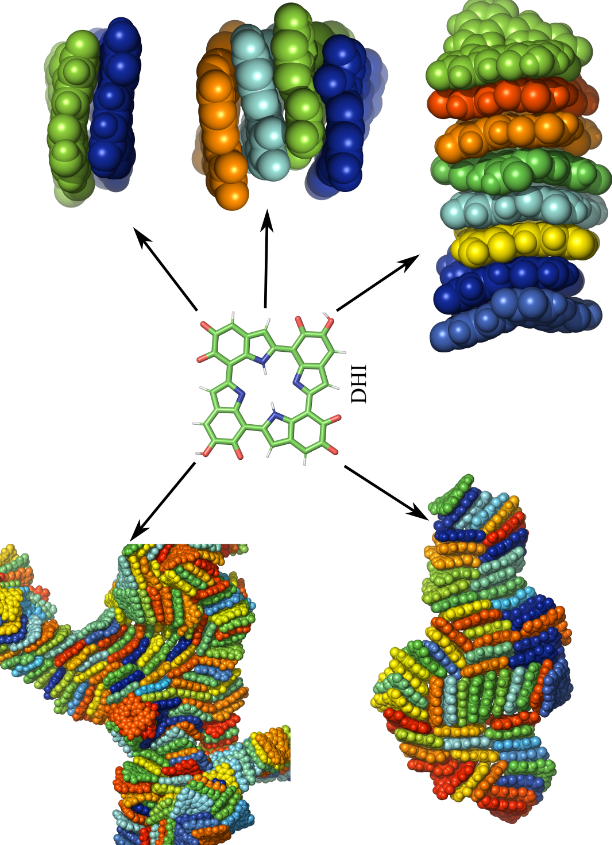
The curious structure of eumelanin and how drugs bind to it Project descriptionMelanins are dark, insoluble biological pigments that are found in a wide range of organisms, including fungi and bacteria, as well as in the tissues of plants, animals, and humans in particular in the eye, skin, hair, and even the inner ear. The three primary melanin types are brown-black eumelanin, yellow-reddish pheomelanin, and dark neuromelanin. Eumelanin, the more abundant type, has various levels of chemical and geometrical disorders, composed of various oxidized 5,6-dihydroxyindole-2-carboxylic acid (DHICA) and/or 5,6-dihydroxyindole (DHI) moieties linked into small oligomers. Melanin has the ability to absorb UV-visible light over a broad spectrum, act as an antioxidant, neutralize free radicals, provide photoprotection, and transfer charge. As a result of these features, applications in diverse sectors such as bioelectronics, batteries, and biomimetic interfaces have gained increasing interest. Interestingly, melanin has been linked to a number of diseases and conditions, including Parkinson’s (in treating it!), age-related/noise-induced hearing loss, and age-related macular degeneration. It is well established that various drugs bind to melanin. The exact mechanism of drug binding is remains, however, unknown. We use Density Functional Theory (DFT) calculations, molecular docking, and Molecular Dynamics (MD) simulations to understand molecular interactions between melanin, various drugs, and the mechanism(s) of drug binding. Such knowledge is critical for reducing the time, cost, and even more importantly, animal testing in drug development. References:
|

|
Carbon to Metal Coating Institute (C2MCI) collaboration Project descriptionThe C2MCI is multi-party Institute with the general aim to develop coating materials for metals. The Institute takes a comprehensive approach to this very broad problem with the particular goals in enhancing the stability of metals used for transportation, green energy, microelectronics and, perhaps surprisingly, finding therapeutics for cancer treatment. References:
|
|
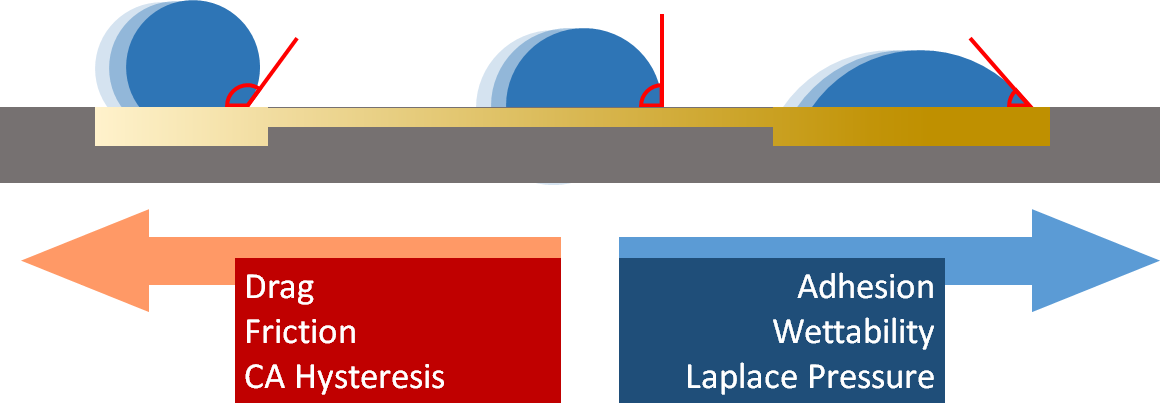
Droplets here, there and everywhere: MD simulations and machine learning to understand transport and detection sensitivity of lab-on-a-chip devices Project descriptionDroplets have a significant impact on our world. They play a crucial role in technologies utilizing sprays and aerosols. Lab-on-a-chip devices provide the setting for small-scale laboratories using droplets. Lab-on-a-chip devices are microchips of sizes less than a few square centimeters with samples that are picolitre (\(10^{-12}\,\)liters)-sized droplets. Despite their minuscule sizes, these miniature laboratories can perform various tasks, such as sample extraction and protein analysis, and as a consequence, they have shown great promise for fast and cheap diagnosis of viral diseases, including HIV, Ebola, and SARS-COV-2. Such devices are crucial for response plans of public health authorities for rapid viral disease diagnosis to avoid pandemics. Droplet-based devices can transport droplets containing samples using external fields. For instance, electric fields, temperature differences, and surface roughness are used to propel droplets at these scales. Surfaces that utilize this method are called gradient surfaces. Simple model systems have used gradients to stretch DNA Giri et al., 2016 or move even droplets uphill F. Wang et al., 2022. However, the design and physical mechanisms of such systems are not well understood. In our study, we use molecular simulations coupled with machine learning to model lab-on-a-chip devices. The goal is to overcome low detection sensitivity problems that arise from small sample sizes. The particlar questions include 1) how the sample, that can, for example contain viruses, behaves within the droplet and how the sample can be loaded. 2) The physical properties of the gradient surface(s) must be understood better, and 3) how the sample can be delivered in a targetted fashion, for example, via desolvation methods. As a little curiosity, droplet speading was the first research problem studied by the PI, see Nieminen et al. below.
|
|
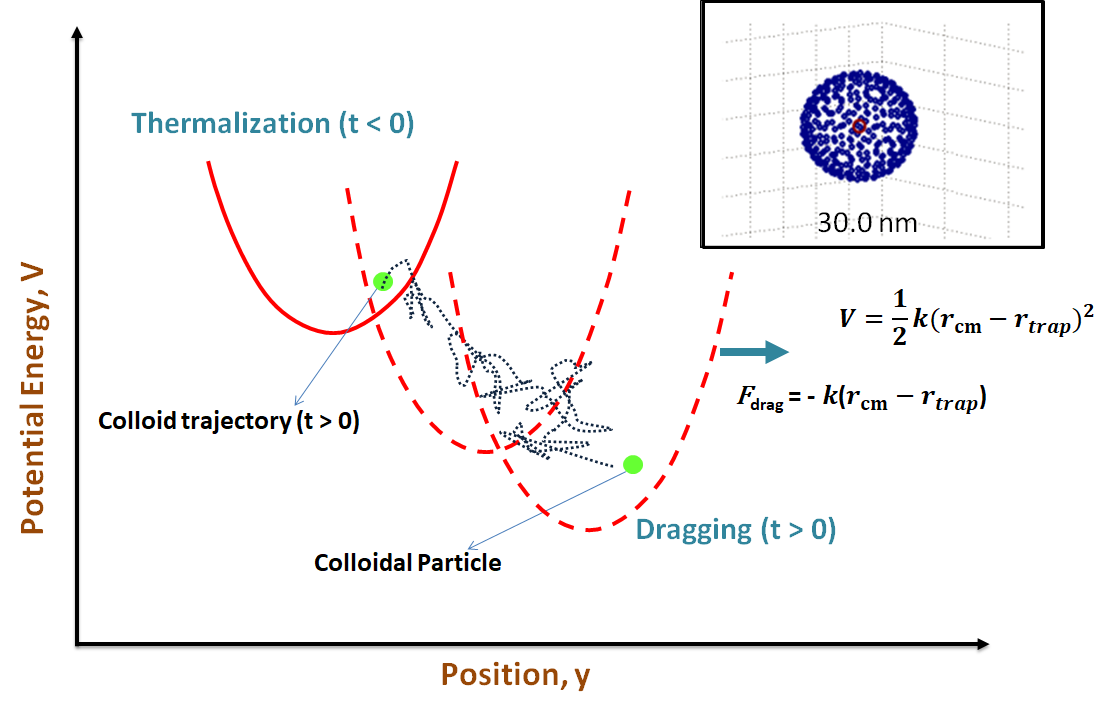
Nonequilibrium modeling of chemical, biological and electrochemical systems with thermal and hydrodynamic fluctuations Project descriptionThermal and hydrodynamic fluctuations, arising as a result of the stochastic nature of molecular collisions and interactions, play an important role in the nonequilibrium dynamics of mesoscale chemical, biological and electrochemical systems. With advances in nanotechnology, these fluctuations present both an unprecedented opportunity and a challenge for controlling chemical reactions and soft matter on the nanoscale. Landau and Lifshitz proposed a solution for the introduction of thermal fluctuations in the Navier-Stokes equations for fluids already back in 1957. However, even after the passage of more than six decades, the modeling and simulation of nonequilibrium chemical and electrochemical phenomena with fluctuations has remained a formidable task. Quantum mechanical and molecular dynamics simulations allow for a simulation of such phenomena in unprecedented detail but are computationally so expensive as to make it almost impossible to simulate nanoscale device or system level dynamics on relevant length and timescales in any meaningful manner. Therefore, there is a need to develop multiscale coarse-grained simulation methods for modeling nonequilibrium chemical, biological and electrochemical systems. As part of this project, we aim to develop Lattice-Boltzmann algorithms in conjunction with materials modeling and machine-learning to develop coarse-grained multiscale methods to model and simulate confined chemical, biological and electrochemical systems in the presence of fluctuations. The development of these coarse-grained methodologies will go significantly beyond the current-state-of the-art and help advance a fundamental understanding of the role of thermal and hydrodynamic fluctuations in the nonequilibrium dynamics of confined mesoscale chemical, biological and electrochemical systems. This in turn will lead to the development of novel strategies for exploiting such phenomena in applications ranging from nanocatalysis, high-efficiency solar thermophotovoltaics, point-of-care lab-on-chip bioelectrochemical analysis and diagnostics, colloidal or molecular self-assembly, targeted drug delivery or cargo transport using artificial swimmers, to, nanoscale stochastic heat engines and beyond. References:
|